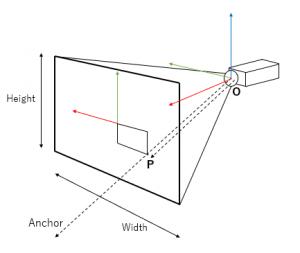
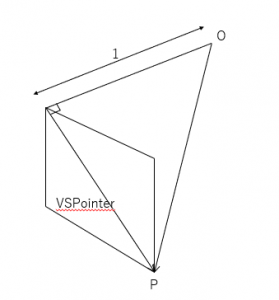
bool UDragSkyUtils::CalcCameraRotationFromAnchor(FRotator &Result, const FVector &AnchorVector, const FVector2D &PointerUV, float FovXInDegree, float AspectRatio)
{
const float FovX = FMath::DegreesToRadians(FovXInDegree);
//
// VirtualScreen(VS) : viewport projected toward the plane in front of camera in distance of 1.0
//
const FVector2D VSPointerNormalized = (PointerUV - FVector2D(0.5f, 0.5f)).ClampAxes(-0.5f, 0.5f);
const float VSWidth = 2.0f*FMath::Tan(FovX*0.5f);
const float VSHeight = VSWidth / AspectRatio;
const FVector2D VSPointer = VSPointerNormalized * FVector2D(VSWidth, VSHeight);
const float AnchorDepth = AnchorVector.Size() / FMath::Sqrt(1.0f + FMath::Square(VSWidth*VSPointerNormalized.X) + FMath::Square(VSHeight*VSPointerNormalized.Y));
// Anchor vector projected onto VirtualScreen
const FVector ProjectedAnchorVector = AnchorVector / AnchorDepth;
// Alias for simple expression
const FVector &P = ProjectedAnchorVector;
const FVector2D &S = VSPointer;
FVector CameraRight;
{
// ProjectedAnchor dot Right = VSPointer.X
// -> W.X*Right.X + W.Y*Right.Y = S.X
// Right.Size() = 1
// -> Right.X*Right.X + Right.Y*Right.Y = 1
// Right.Z = 0
//
const float A = P.X*P.X + P.Y*P.Y;
const float RightX1 = (S.X * P.X + P.Y*FMath::Sqrt(A - S.X * S.X))/A;
const float RightX2 = (S.X * P.X - P.Y*FMath::Sqrt(A - S.X * S.X))/A;
const float RightY1 = (S.X * P.Y - P.X*FMath::Sqrt(A - S.X * S.X))/A;
const float RightY2 = (S.X * P.Y + P.X*FMath::Sqrt(A - S.X * S.X))/A;
const FVector Right1(RightX1, RightY1, 0.0f);
const FVector Right2(RightX2, RightY2, 0.0f);
const FVector TemporaryForward = AnchorVector;
if (FVector::CrossProduct(TemporaryForward, Right1).Z >= 0)
{
CameraRight = Right1;
}
else
{
CameraRight = Right2;
}
if (CameraRight.ContainsNaN())
{
UE_LOG(LogTemp, Log, TEXT("Right vector contains nan"));
return false;
}
}
FVector CameraForward, CameraUp;
{
// ProjectedAnchor dot Up = VSPointer.Y
// -> W.X*Right.X + W.Y*Right.Y = S.Y
// Up.Size() = 1
// -> Up.X*Up.X + Up.Y*Up.Y + Up.Z*Up.Z = 1
// Up dot Right = 0
//
const FVector &R = CameraRight;
const float C = (P.X*R.Y - P.Y*R.X);
const float Determinant = FMath::Square(C*S.Y / (C*C + P.Z*P.Z)) - (S.Y*S.Y - P.Z*P.Z) / (C*C + P.Z*P.Z);
if (Determinant<0.0f)
{
UE_LOG(LogTemp, Log, TEXT("Determinant : %f"), Determinant);
return false;
}
const float F1 = -(C*S.Y) / (C*C + P.Z*P.Z) + FMath::Sqrt(Determinant);
const float F2 = -(C*S.Y) / (C*C + P.Z*P.Z) - FMath::Sqrt(Determinant);
const FVector Up1(-R.Y*F1, R.X*F1, FMath::Sqrt(1.0 - F1 * F1));
const FVector Up2(-R.Y*F2, R.X*F2, FMath::Sqrt(1.0 - F2 * F2));
const FVector Forward1 = FVector::CrossProduct(R, Up1);
const FVector Forward2 = FVector::CrossProduct(R, Up2);
const float Dot1 = FVector::DotProduct(Forward1, P);
const float Dot2 = FVector::DotProduct(Forward2, P);
const float Diff1 = FMath::Abs(Dot1 - 1.0f);
const float Diff2 = FMath::Abs(Dot2 - 1.0f);
const float MinDiff = FMath::Min(Diff1, Diff2);
if (MinDiff > 0.001f)
{
UE_LOG(LogTemp, Log, TEXT("No solution found"));
return false;
}
if (Diff1 < Diff2)
{
CameraUp = Up1;
CameraForward = Forward1;
}
else
{
CameraUp = Up2;
CameraForward = Forward2;
}
if (CameraUp.ContainsNaN())
{
UE_LOG(LogTemp, Log, TEXT("NaN detected"));
return false;
}
if (CameraForward.ContainsNaN())
{
UE_LOG(LogTemp, Log, TEXT("NaN detected"));
return false;
}
}
FMatrix RotMatrix(CameraForward, CameraRight, CameraUp, FVector::ZeroVector);
Result = RotMatrix.Rotator();
if (Result.ContainsNaN())
{
UE_LOG(LogTemp, Log, TEXT("rotator contains nan"));
return false;
}
return true;
}

 [UE5]マテリアルのSDFとは?画像から考える距離場のしくみ
2025.12.03UE
[UE5]マテリアルのSDFとは?画像から考える距離場のしくみ
2025.12.03UE
 [UE5]Color CurveをMaterial Functionで設定するには
2025.04.09その他
[UE5]Color CurveをMaterial Functionで設定するには
2025.04.09その他
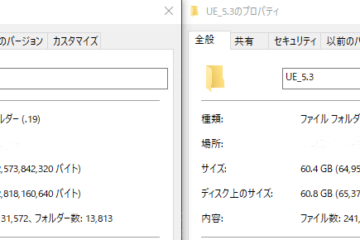
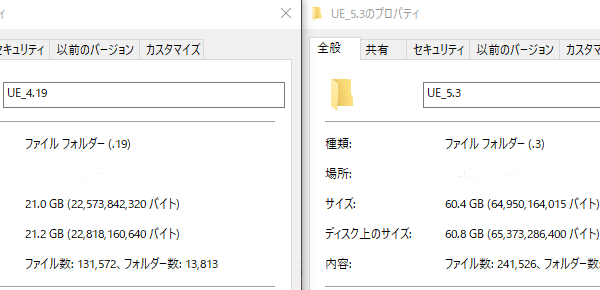 [UE4][UE5]開発環境の容量を少しでも減らす
2024.08.14UE
[UE4][UE5]開発環境の容量を少しでも減らす
2024.08.14UE