0.概要
「複数のキャラクター全てをぴったり画面に収める」
個人的な経験から言うと、使いそうであんまり使わない、でも時々欲しくなることもある・・・そんな機能だと思います。
これを実現するため、カメラの配置について以下の要件を満たすことを考えます。
・カメラの向き及び視野角は予め決まっている
・空間内で任意の座標を持つポイントが複数与えられる
・画面内の端から指定した割合のエリアを除いた部分(以下”セーフフレーム”)に与えられた全てのポイントを含む
・可能な限り前に寄る(⇒セーフフレームの左右両方、または上下両方に与えられた点のいずれかが接する)
つまりこういうことです↓
明るい枠内に4つの球体がぴったり収まるようカメラの位置を制御しています。
ここでは気持ちよく、とか良い感じに、とかいった些末については無視して、
とにかくぴったり収めるためのロジックとその実装についてのみ触れます。
内容は数学・・・というか幾何学ですが、なるべく図を入れているので苦手な方でも雰囲気をつかめるかもしれません。
「ドット積(ベクトルの内積)」あたりを抑えていれば普通に読めると思います。
末尾にサンプルコードを添付していますが、これについてはC++を扱えることが必須です。
では解決していきましょう。
あ、演習問題としても悪くない内容だと思いますので、挑戦されたい方は答えを見る前に是非・・・!
1.理論編
説明がややこしくなるのでセーフフレームのことは一旦忘れます。
この手の問題の常として、まずは「視界内に全ての点が収まる」とはどういうことかを数式で表現できるように消化する必要があります。
とりあえず点が一つの場合を考えます。
視界内に点が収まる
↓
カメラの位置から前方に広がる四角錐にその点が含まれる
↓
四角錐を構成する全ての面に対して点が表側(ここでは四角錐の内側を面の表としました)に位置する
↓
『全ての面について
dot(カメラの座標, 面の法線ベクトル) ≦ dot(点の座標, 面の法線ベクトル)
が満たされる
(dot(a, b) は ベクトル a, b のドット積)』・・・①
このように置き換えられます。
点が複数存在することを加味すると、
『全ての面について
dot(カメラの座標, 面の法線ベクトル) ≦ min(dot(点1の座標, 面の法線ベクトル), dot(点2の座標, 面の法線ベクトル), …)
が満たされる
(min(a,b,c,…) は スカラー値 a, b, c, … のうち最小の値)』・・・②
こうなります。
数式だけではよく分からないかもしれません。
確認の意味も込めて作図してみます。
視認性のために二次元から始めます(途中から三次元になります)。
カメラの向きと視野角が既知であることより、面の法線ベクトルは確定しています。
しかし、面の位置は分かりません。これから求めようとしているカメラの座標と連動するからです。

Fig. 01. 面の法線ベクトル
この面をAとします。
そこに、カメラに収めたい点を置きます。
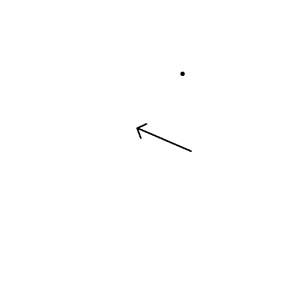
Fig. 02. 面Aの法線ベクトルと点
ここにカメラを追加することを考えます。
①より
dot(カメラの座標, 面の法線ベクトル) ≦ dot(点の座標, 面の法線ベクトル)
を満たすカメラの座標は下図のように示されます。
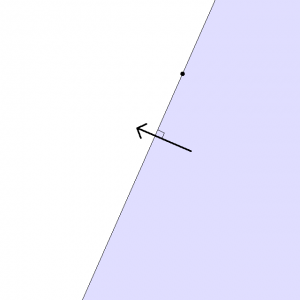
Fig. 03. カメラを置けるエリア(水色部分)
点が増えるとどうなるでしょうか。
以下の条件を満たすエリアはどこでしょう。
②より
dot(カメラの座標, 面の法線ベクトル) ≦ min(dot(点1の座標, 面の法線ベクトル), dot(点2の座標, 面の法線ベクトル), …)
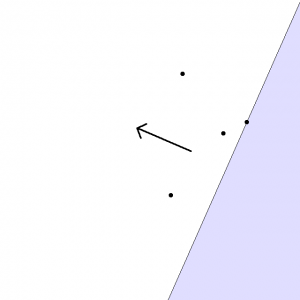
Fig. 04. カメラを置けるエリア(点が複数ある場合)
さらに、面Bを追加します。
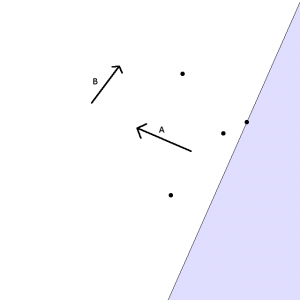
Fig. 05. 面(B)を追加
面Bについて条件を満たすエリアは下図のようになります。
(この形だと、画像のなんとなく上方がカメラの正面方向ということになります。)
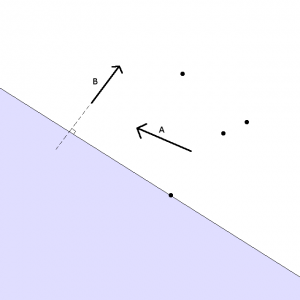
Fig. 06. カメラを置けるエリア(面Bについて・水色部分)
カメラは全ての面について条件を満たす位置に置かれなくてはなりません。
つまり、Fig.05.とFig.06.の水色の重なる部分ということになります。
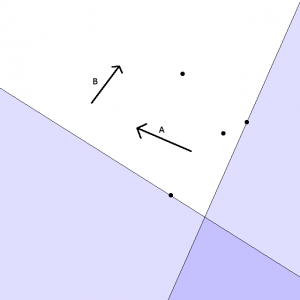
Fig. 07. カメラを置けるエリア(濃い水色部分)
上記のように、二辺に挟まれたエリアが該当することになります。
三次元的に考えた場合、二辺ではなく二面に挟まれたボリュームとなります。
図示が難しくなってきますが、下のような感じです。
(波線の部分は無限に続くべきところを省略したものとして見て下さい)
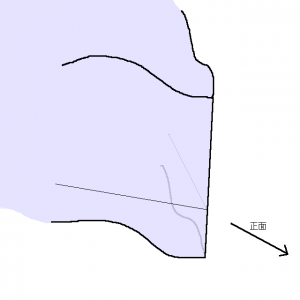
Fig. 08. カメラを置けるエリアの形状(面A、面Bを考慮)
Fig.08.の水色部分はFig.07.の濃い水色部分に該当します。
残りの2面をも考慮に入れると下図のようになります。
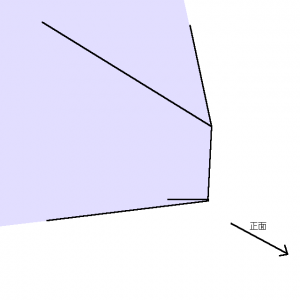
Fig. 09. カメラを置けるエリアの形状(4面を考慮)
点が画面の左右端に接する場合と上下端に接する場合とで先端の形状に違いが出ます。
やはり先端の辺上が最もカメラを寄せた位置ということになります。
そしてこの辺は、左右および上下の面のみを考慮した場合の最寄り配置(カメラにとって縦と横に伸びる無限直線)のうち、より後方に位置するものの一部です。
点群の画面への収まり方をなるべく偏らせたくないという条件を加味すると、カメラを配置すべき位置を絞り込むことができます。
右や左に点が偏らないように配置すべきと考えると、最も寄った(左右いっぱいに使う)配置を表す辺から真っすぐ後方に引いた位置の集合が一つの候補になるでしょう。
図にすると以下のようになります。
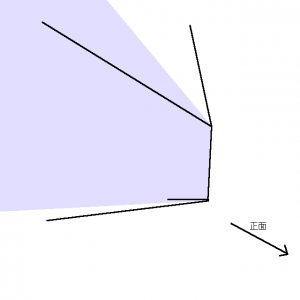
Fig. 10. だいたい左右均等に点群を収められるカメラ位置
上下の面についても同様の手順で平面(こんどは水平になります)が決まり、これらの交わる範囲がカメラの配置先ということになります。
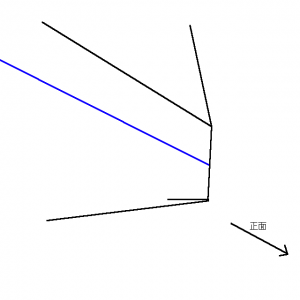
Fig. 11. 最終的なカメラの配置範囲
その交わる範囲はFig.11.に青く示したようにカメラの後方に伸びる半直線になります。
できるだけ被写体に寄せるという条件であれば、前方の端点が解ということになります。
最後にセーフフレームについてですが、
射影後の画面内にて端を除外するということは視野角を狭めるということと同じであるため、特別なロジックを必要としません。
ここまで視野角としていた部分をセーフフレームの分狭めた値に置き換えるのみでOKです。
大雑把な理論についてはここまでで完成です。
2.実装編(ソースコードとコメント)
原理について書いてしまったのでここで語ることはとくにありません。
補助程度にコメントを付けてありますので一助になればと思います。
ノリでいくつか要素を追加していますが、基本的な理屈は1.で説明した通りですので流したり解析したりしてみてください。
UE4向けのコードとして書いてありますが、数学系の補助関数を用いている程度ですので少し改修をすれば任意の環境で通じるはずです。
アプリケーション的な部分は含めず、単に座標を返す関数の定義に留めています。
// Pointsで与えられた座標群をNormal軸へ射影した結果のうち最小のものを取得します(ついでに大きさを考慮したオフセットを行います)。
float GetMinProjection(FVector Normal, const TArray<FVector> &Points, const TArray<float> &Sizes)
{
float Retval = MAX_FLT;
for (int i = 0; i < Points.Num(); ++i)
{
Retval = FMath::Min(Retval, FVector::DotProduct(Points[i], Normal) - Sizes[i]);
}
return Retval;
}
// ターゲットの位置・大きさおよびカメラの向きから最適なカメラの位置を決定
FVector CalcCameraLocationByTargetPoints(const TArray<FVector> &Points, const TArray<float> &Sizes, const FRotator CameraRotation, const float FovXDegrees, const float AspectRatio, const float FovLeftMargin, const float FovRightMargin, const float FovBottomMargin, const float FovTopMargin)
{
const float HalfFov_X = FMath::DegreesToRadians(FovXDegrees*0.5f);
const float HalfTanX = FMath::Tan(HalfFov_X);
const float HalfTanY = HalfTanX / AspectRatio;
// 非対称なセーフフレームをサポート
// セーフフレームの視野角を上下左右について求めます
const float HalfFovLeft = FMath::Atan(HalfTanX * (1.0f - FovLeftMargin * 2.0f));
const float HalfFovRight = FMath::Atan(HalfTanX * (1.0f - FovRightMargin * 2.0f));
const float HalfFovBottom = FMath::Atan(HalfTanY * (1.0f - FovBottomMargin * 2.0f));
const float HalfFovTop = FMath::Atan(HalfTanY * (1.0f - FovTopMargin * 2.0f));
const float HalfFovLeftDeg = FMath::RadiansToDegrees(HalfFovLeft);
const float HalfFovRightDeg = FMath::RadiansToDegrees(HalfFovRight);
const float HalfFovBottomDeg = FMath::RadiansToDegrees(HalfFovBottom);
const float HalfFovTopDeg = FMath::RadiansToDegrees(HalfFovTop);
// 座標軸をカメラのそれと平行にすることで計算を簡略化できます。
// 原点はそのまま、回転のみ合わせます
// カメラの座標が原点ではないことに注意。
TArray<FVector> PointsCS;
PointsCS.SetNum(Points.Num());
for (int i = 0; i < Points.Num(); ++i)
{
PointsCS[i] = CameraRotation.UnrotateVector(Points[i]);
}
// ここに計算結果を格納します
FVector CameraLocationCS;
// 左右の面による拘束
float XbyLR;
float Dydx;
{
// カメラと平行な座標系では、XY平面上で計算できます
const FVector LeftBoundNormalCS = FVector::RightVector.RotateAngleAxis(-HalfFovLeftDeg, FVector::UpVector);
const float LeftBoundPosCS = GetMinProjection(LeftBoundNormalCS, PointsCS, Sizes);
const FVector RightBoundNormalCS = -FVector::RightVector.RotateAngleAxis(HalfFovRightDeg, FVector::UpVector);
const float RightBoundPosCS = GetMinProjection(RightBoundNormalCS, PointsCS, Sizes);
// 連立方程式を解きます。
// Q は XY平面上に射影した左右の面の交点です
// dot(Q, LeftBoundNormalCS) = LeftBoundPosCS
// dot(Q, RightBoundNormalCS) = RightBoundPosCS
//
// 整理して以下の式を得られます
const float QX = (RightBoundNormalCS.Y*LeftBoundPosCS - LeftBoundNormalCS.Y*RightBoundPosCS) / (LeftBoundNormalCS.X*RightBoundNormalCS.Y - LeftBoundNormalCS.Y*RightBoundNormalCS.X);
const float QY = (LeftBoundPosCS - QX * LeftBoundNormalCS.X) / LeftBoundNormalCS.Y;
// 一時的に解を格納します。
// Xは一時的な値で、上下の面の条件から得られる値との比較が必要です。
// Yはこれで決まりです。
// Zは上下面の条件を調べるまで分かりません。
XbyLR = QX;
CameraLocationCS.Y = QY;
// Xに対するYの変化量(セーフフレーム非対称性への対処)を保存します
Dydx = HalfTanX * (FovLeftMargin - FovRightMargin);
}
// 上下の面による拘束
float XbyTB;
float Dzdx;
{
// XZ平面上で計算できます
const FVector BottomBoundNormalCS = FVector::UpVector.RotateAngleAxis(-HalfFovBottomDeg, -FVector::RightVector);
const float BottomBoundPosCS = GetMinProjection(BottomBoundNormalCS, PointsCS, Sizes);
const FVector TopBoundNormalCS = -FVector::UpVector.RotateAngleAxis(HalfFovTopDeg, -FVector::RightVector);
const float TopBoundPosCS = GetMinProjection(TopBoundNormalCS, PointsCS, Sizes);
// 左右面のときと同様です。
const float QX = (TopBoundNormalCS.Z*BottomBoundPosCS - BottomBoundNormalCS.Z*TopBoundPosCS) / (BottomBoundNormalCS.X*TopBoundNormalCS.Z - BottomBoundNormalCS.Z*TopBoundNormalCS.X);
const float QZ = (BottomBoundPosCS - QX * BottomBoundNormalCS.X) / BottomBoundNormalCS.Z;
// 左右、上下の条件から得たXのうち小さい方(より後ろへ引いた方)が求める値です。
XbyTB = QX;
CameraLocationCS.Z = QZ;
// Xに対するZの変化量(セーフフレーム非対称性への対処)を保存します
Dzdx = HalfTanY * (FovBottomMargin - FovTopMargin);
}
CameraLocationCS.X = FMath::Min(XbyLR, XbyTB);
CameraLocationCS.Y += (Dydx * (CameraLocationCS.X - XbyLR));
CameraLocationCS.Z += (Dzdx * (CameraLocationCS.X - XbyTB));
// World座標に復元して返します
return CameraRotation.RotateVector(CameraLocationCS);
}
|
3.まとめ
向きの予め決められたカメラを、複数の任意の点を画面内に収めるよう配置する方法について一つの考え方を示しました。
以上です。
 [UE5]Color CurveをMaterial Functionで設定するには
2025.04.09その他
[UE5]Color CurveをMaterial Functionで設定するには
2025.04.09その他
 [UE4][UE5]開発環境の容量を少しでも減らす
2024.08.14UE
[UE4][UE5]開発環境の容量を少しでも減らす
2024.08.14UE

 [UE5] PushModel型のReplicationを使い、ネットワーク最適化を図る
2024.05.29UE
[UE5] PushModel型のReplicationを使い、ネットワーク最適化を図る
2024.05.29UE



















