[UE4] VolumeDecalによる多面体表示

執筆バージョン: Unreal Engine 4.24

概要

UE4の実験的機能の一つである”Volumetric Distance Function”を使って正多面体を表示しつつ色々と学ぶための記事です。

過去の記事でも扱いはしましたが、今回は具体的な例をとることでより分かりやすくなっている・・・かもしれません。

[UE4] VolumeDecal (Experimental) を使ってみる

 

準備

１．マテリアル

マテリアルを作成し、以下のように設定します。

Decal Blend Mode の部分が今回の肝です。

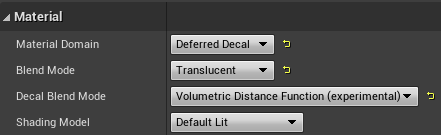
以下のように組みます。

 

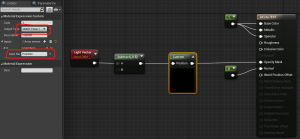
２．ブループリント

プレビュー用のブループリントを作成します。

ActorブループリントにDecalコンポーネントを追加し、

先程作成したマテリアルを設定します。

 

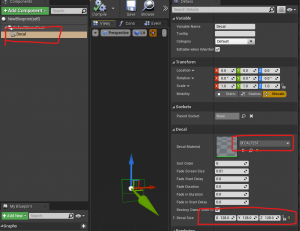
これをテンプレートとして様々な図形を表示します。

 

図形の作成

距離関数というものについて軽く説明しておきます。

DecalBlendMode = VolumetricDistanceFunction のとき、

OpacityMaskに「LightVectorで受け取った位置から表示したい面までの距離っぽいもの」を出力することでレイマーチング処理によって形状が描画されます

（なおDecalマテリアル一般のルールとして、LightVectorにはDecalボリューム内の座標が(0,0,0)~(1,1,1)に正規化されて入力されています）。

このOpacityMaskに出力しているのがいわゆる距離関数と呼ばれるものです。

 

マテリアルの中でも独特の手法ですので少し慣れが必要です。

 

０．球

準備運動として球を作成してみましょう。

 

ある点Pから球体(中心O, 半径R)の表面までの距離Dは

D = length(P-O) – R

（lengthはベクトルの長さを返す関数）

と表せます。

Dが負の場合は点が内部にあることを表します。

 

今回は簡単のため球の中心を原点に一致させておきます。

準備で作成したテンプレートのCustomを複製して以下のように編集、Applyするとブループリントのビューポート上で結果を確認できます。

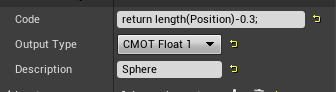
ポリゴンベースのものと異なり「カド」の出ないきれいな球体が表示されます。

 

１．立方体

ここからが本題です。

任意の点から立方体表面までの距離はどのように表せるでしょうか。

真面目に考えると、立方体の中で与えられた任意の点に最も近い点が

①面上にある場合

②辺上にある場合

③頂点の場合

によって計算が異なり、けっこう面倒なことになります。

立方体だけならまだしも、他の多面体のことまで考えるととても手に負えません。

 

ここで距離関数について先程「表示したい面までの距離っぽいもの」と表現しましたが、

レイマーチングの仕組み上、これが実際の距離より多少短い分には問題ありません（なるべく近いに越したことはありませんが）ので、近似を考えます。

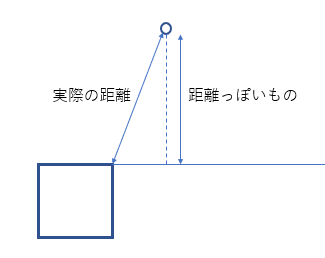
上の図から何となく分かるように、元の面を無限に拡張した面と点との距離（距離っぽいもの）は、かならず本来の距離以下におさまります。

よって全ての面についてこの距離っぽいものを求め、その最大値を最終的に用いる距離っぽいものとして採用します。

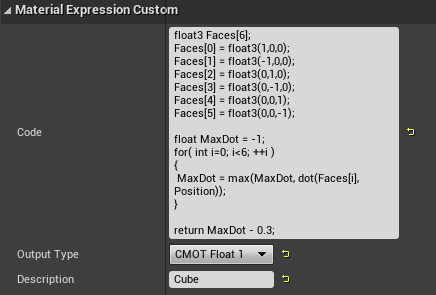
ある面に対する距離っぽいものをDとすると

D = dot(N, P) – R

（dotはドット積、Nは面の法線ベクトル、Rは中心から面までの距離）

となるので、その最大値を用いるわけです。

 

２．正八面体

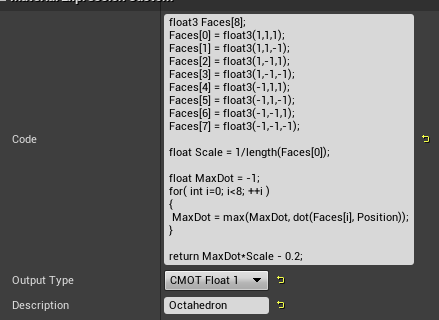
前項のコードを読めば分かると思いますが、

Facesの中身とループ回数を変えるだけで終わります。

正八面体各面の法線ベクトルは勘で分かると思います。

正規化した値を書くのは面倒なので、最後の行で正規化の計算を行っています(*Scale)。

 

３．正四面体

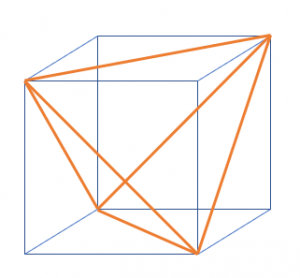
正四面体はどうでしょう。

XY平面に素直に立つ図を考えるとけっこう面倒な計算になりますが、

立方体の8頂点から一つとびに4つ取り出す感じで考えると簡単です。

 

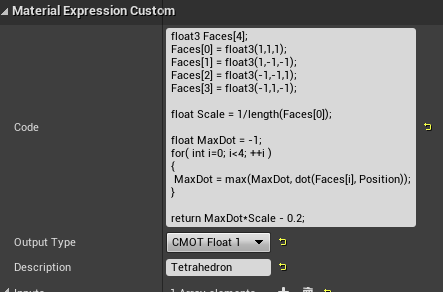
あとたったの2個です、がんばりましょう！

 

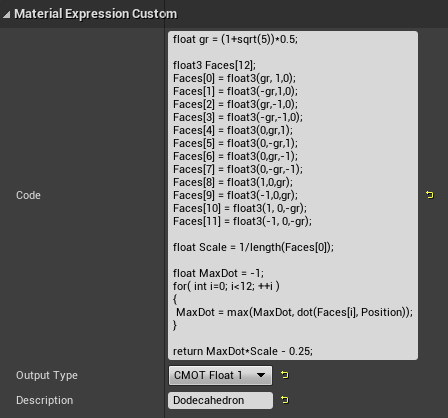
４．正十二面体

正十二面体がどういう図形かお分かりでしょうか。

正五角形が12個くっついてできたアレです。

参考画像

その法線となると・・・？

頂点の座標は適当にぐぐると見つかりますが、法線の向きまではなかなか出てきません（どこかにあるかもしれませんが）。

頂点を使ってクロス積で法線を・・・？

否、もっと簡単な方法があります。

正多面体同士には双対関係というものがあり、例えば正十二面体の面の中心を結ぶと正二十面体が得られます。

則ち、正二十面体の頂点の座標をそのまま正十二面体の法線ベクトルとして利用できます。

正二十面体の頂点の座標は

(0, ±1, ±ϕ)

(±1, ±ϕ, 0)

(±ϕ, 0, ±1)

（ϕは黄金比 = (1+sqrt(5))/2、±は任意の組み合わせ）

と表現できます。

とらえどころのないように見えて、意外と軸に沿った感じですね。

黄金比が登場するところも興味深いです。

 

５．正二十面体

これはもう正十二面体のときの逆ですね。

双対となる正十二面体の頂点は

(0, ±1/ϕ, ±ϕ)

(±1/ϕ, ±ϕ, 0)

(±ϕ, 0, ±1/ϕ)

(±1, ±1, ±1)

（ϕは黄金比 = (1+sqrt(5))/2、±は任意の組み合わせ）

です。

コードがちょっと長くなりますが、

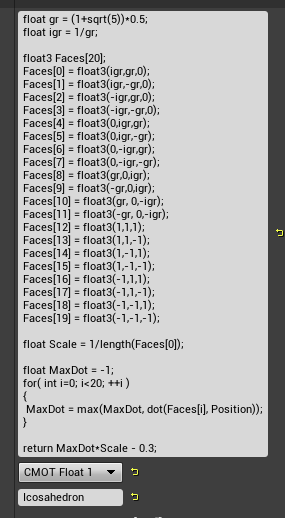
このようになります。

 

まとめ

全ての正多面体についてVolumeDecalで表示する方法について紹介しました。

 

追記０１

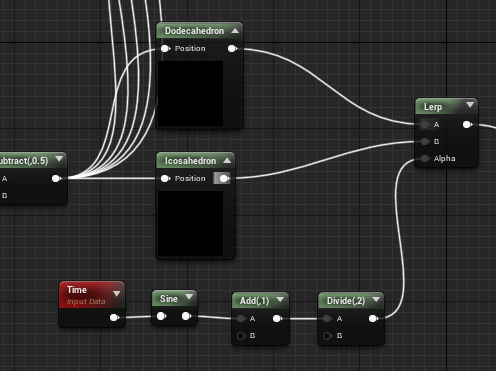
↑のように、単に距離関数同士を線形補間するだけで形状と形状の補間が得られます。

多面体同士もいいですが、球体とのブレンドも魅力的な形状になります。

 

追記０２

既にお気づきの方も多いと思いますが、実は正多面体のみならず任意の凸型多面体に応用可能な手法です。

形状データを【法線+中心からの距離】を表すピクセルの集合としてテクスチャに保存することで、モデリングしたものを持ち込むことも可能でしょう。

 

追記０３

現在バージョン(4.24で確認)において、VolumeDecalの深度情報が上手く書き込まれない問題があり、空間において背景と重なる場合に正しく表示されなかったりします。

修正にチャレンジするのも一興かもしれません。